Wojciech Broniowski and Wojciech Florkowski
The H. Niewodniczański Institude of Nuclear Physics, PL-31342 Cracow, Poland.
(Recieved 9 October 2001; published 25 January 2002)
우리는, 상대론적인 중이온 충돌에서 잘 만족하는 일반적인 가정들 하에서 중심도 c와 충격 변수 b사이의 기하학적 관계 \(c\simeq\pi b^2/\sigma_\text{inel}\)이 매우 얇은 충돌(most peripheral collision)인 경우를 제외하고는 매우 높은 정확도로 만족한다는 것을 보여 줄 것이다. 더 정확히, 만약 \(c(N)\)이 \(N\)보다 큰 다중도(multiplicity)를 가진 사건들의 중심도라면, b는 평균 다중도 \(n(b)\)가 \(N\)과 같을 때의 충격 변수 값이다. 이 기하학적 공식의 보정치는 \((\Delta n(b)/n(b))^2\)이며, \(\Delta n(b)\)는 주어진 \(b\)값에서의 다중도 분포의 너비이기 때문에 두 값들은 매우 작다. 다른말로, 중심도는 사실상 충격 변수와 같다.
DOI: 10.1103/PhysRevC.65.024905 PACS number(s): 25.75.Dw, 25.75.Ld, 24.10.-i
상대론적 중이온 충돌의 데이타는 보통 중심도 \(c\)를 이용해서 분류된다. 중심도 \(c\)는, (검출기에 측정된) 생성된 입자들이 가장 많거나 (영도열량계(zero-degree calorimeter)로부터 정해진) 충돌에 참여한 핵자들의 수가 가장 많은 사건들의 백분위수로 정의한다. 우리는 이 사건들의 숫자를 일반적으로 \(n\)으로 나타낸다. 그 다음, 다중도[1,2], \(p_\perp\) 스펙트럼[3-5], 타원 흐름 계수 \(v_2\)[6,7], HBT 반지름[8] 등과 같은 측정 결과들을 다양한 중심도에 대해 나타낸다. 실험적인 관점에서, 중심도는 애매하지 않고 좋은 기준으로 데이타를 나눌 수 있게 해준다. 반면, 이론학자들은 충격 변수 \(b\)를 주어진 중심도에 맞게 대응시킬 필요가 있다. 충격변수는, 충돌의 초기 기하학적 구조를 줄 뿐 아니라 충돌의 공식화 과정에 두루 나타나기 때문에, 어떤 면에서는 더 기본적인 값이라고 할 수 있다. 중이온 물리학의 이론적 계산에서는, 실험 결과를 예측하기 위해 \(b\)를 사용한다. 계산을 끝내고 나면, 모델의 결과를 어떤 중심도 데이타와 비교해야 하는지에 대한 문제가 발생한다. 이것을 해결하기 위해, 사람들은 상처입은 핵자들의 수나 주어진 \(b\)에서의 두입자 충돌(binary collision)의 수를 계산하기 위해 Glauber 모델을 사용하는데, 결국 다중도나 충돌에 참여한 핵자들의 수와 관련이 있게 된다.[9,10]. 결국 이러한 것들은 실험에서 측정되기 때문에, \(c\)를 가지고 \(b\)를 알아낼 수 있다.
우리는 이 논문에서 그러한 노력이 필요 없다는 것을 보여 줄 것이다. 왜냐하면 상대론적 중이온 충돌에서 매우 잘 만족하는 일반적인 가정들 하에서 매우 높은 정확도로 다음 관계식이 성립하기 때문이다.
\[c(N)\simeq\frac{\pi b(N)^2}{\sigma_\text{inel}}\qquad\text{for }b<R.\qquad\qquad(1)\]
위 식에서 \(\sigma_\text{inel}\)은 비탄성 원자핵-원자핵 총 단면적(total inelastic nucleus-nucleus cross section)이고 \(R\)은 충돌하는 원자핵 반지름들의 합의 차수이다. 중심도 \(c(N)\)은 다중도가 \(N\)보다 큰 충돌 사건들의 중심도인 반면, \(b(N)\)은 평균 다중도 \(n(b)\)이 \(N\)과 같을 때의 충격 변수 값이다. 앞으로 보이겠지만, 식 (1)은 매우 얇은 충돌을 제외하고는 매우 높은 정확도로 성립한다. 식 (1)은 그 기하학적인 특성 때문에 (다중도, 충돌에 참여한 핵자 수, 두입자 충돌 수 등의) 데이타를 분류하는데 필요한 변수 \(n\)에 직접적으로 연관되지 않는다. 처음 보기에 이 사실은 좀 놀라울지도 모르겠다.
식 (1)의 기하학적인 특성과 \(n\)에 직접적으로 의존하지 않는다는 사실을 다음 비유적인 예제를 가지고 설명할 수 있다. 반지름이 \(R\)인 과녁을 향해 궁수들이 각각 한번씩 쏘는 시합이 있다고 생각해보자. 궁수들은 활을 너무 못 쏴서 아무데로나 막 쏜다(randomly). 궁수들은 자기가 맞춘 대 대한 보상을 받는데, 더 안쪽을 맞출수록 더 많은 보상을 받는다. 우리는 시합을 볼 수 없게 돼있어서 과녁의 어느 부분에 맞았는지 알 수 없지만 나중에 보상 기록을 볼 수는 있다. 많은 수의 궁수들이 점수를 냈고, (여기엔 지면 문제상 10명만 적지만) 상금순으로 적으면 $100, $100, $50, $50, $50, $10, $10, $10, $10, $10 가 된다. 최고 금액($100)을 받은 두명의 궁수는 과녁의 중심을 맞추었다. 이 숫자는 전체 궁수들의 20%를 차지하고 궁수들은 아무데로나 쏘았기 때문에, (통계 오차를 무시하면) 우리는 바로 과녁의 중심 반지름 \(b\)를 구해낼 수 있다. 전체 과녁 면적의 20%가 중심의 면적이므로: \(20\%=\pi b^2/(\pi R^2)\). 따라서 \(b=R\sqrt{20\%}\)이다. 이제 또다른 시합이 열렸다고 해보자. 이 시합은 전 시합과 보상액만 다르고 모든 규칙은 같다. 열 명의 궁수들이 각각 $500, $500, $100, $100, $100, $50, $50, $50, $50, $50의 보상을 받았다고 가정하면, 우리는 또 20%의 가장 높은 보상들이 과녁의 중심을 맞췄다고 알 수 있고, 중심의 반지름을 전과 똑같이 \(b\)로 정할 수 있다. 주목할점은 우리가 \(b\)를 정하는 과정에서 실제 보상 값을 전혀 사용하지 않았다는 것이다. 다시말해 \(b\)를 구하는데 사용된 함수는 중심도에 대해 단조 함수(monotonic function)이기만 하면 된다. 보상은 단지 데이타를 분류하는데에만 사용된다. 일단 분류가 끝나면, “가장 중심을 맞춘” 궁수들의 \(c\)를 알 수 있고, 분류하는데 사용한 함수와 관계없이 식 (1)에 따라 \(b\)를 정할 수 있다. 우리가 사용한 예제는 중이온 충돌에 다음과 같이 적용할 수 있다: 활쏘기 시합-중이온 충돌 실험, 점수를 기록한 궁수-사건, 시합 1의 보상-충돌에 참여한 핵자들의 수, 시합 2의 보상-생성된 입자들의 다중도, 최고 득점 궁수들의 백분위수-중심도, 과녁 원들의 반지름-충격 변수들.
위 예제는, 상대론적 중이온 충돌의 고전 물리학에서 성립하는 우리 주장의 핵심을 보여준다. 그러나, 추가적으로 생각해야 할 두 가지 특징들이 있다. 첫번째로, 특정한 충격 변수 \(b\)에서의 충돌은, 분포 너비가 \(\Delta n(b)\)이고 평균값이 \(n(b)\)인 분포의 값인 \(n\)을 만들어낸다. 앞으로 보여주겠지만, 일반적으로 \(\Delta n(b)\ll (b)\)일 때 유효한 식 (1)은, 입자 생성의 통계적인 모델로부터 얻어진, 현실적으로 큰 값의 \(\Delta n(b)\)에 대해서도 정확하다. 둘째로, \(b\sim R\)근처에서 경계 효과가 존재한다 – 작은 \(b\)값의 비탄성 충돌 단면적은 검은 디스크에 충돌할 때의 충돌 단면적인 반면, 경계에서는 표적이 점차적으로 투명해진다.
우리는 이제 정식으로 식을 유도할 것이다. \(P(n)\)이, (생성된 입자들의 다중도, 충돌에 참여한 입자들의 수, 두 입자 충돌의 수, 등의) 분류 함수에 대해 \(n\)값을 얻을 확률이라고 하자. 간단히 하기 위해 우리는 앞으로 n을 다중도라고 할 것이다. 중심도 \(c\)는 \(P(n)\)의 누적으로 정의된다. 다시말해,
\[c(N)=\sum^\infty_{n=N}P(n).\qquad\qquad(2)\]
따라서 \(c(N)\)은 다중도가 \(N\)과 같거나 더 큰 다중도를 가진 사건을 얻을 확률이다. 특정한 다중도 값 \(n\)은 여러 충격 변수 \(b’\)의 충돌로부터 얻어질 수 있을것이다; 따라서 다음과 같이 쓸 수 있다.
\[c(N)=\sum^\infty_{n=N}\int^\infty_0\frac{2\pi b’db’}{\sigma_\text{inel}}\rho(b’)P(n|b’).\qquad\qquad(3)\]
위 식에서 \(2\pi b’db’\) 은 충격변수 \(b’\)에서 \(b’+db’\)사이의 고리 면적이고, \(\rho(b’)\)은 충격 변수가 \(b’\)인 (비탄성 충돌) 사건이 일어날 확률이며, \(P(n|b’)\)은 충격 변수가 \(b’\)이라고 가정했을 때 다중도가 \(n\)일 조건부 확률이다. \(\rho(b’)\)함수는 \(b’\)이 \(R\)보다 작은 영역에서는 1이고, 핵 밀도 함수가 가장자리에서 씻겨내려가는 모습과 마찬가지로, \(R\) 주변에서는 부드럽게 0으로 떨어진다. 식 (3)은 명확하다: 주어진 문제의 고전적인 특징들이 요구하듯, \(b’\)과 \(b’+db’\)사이의 고리를 때릴 확률, \(b’\)에서 사건이 일어날 확률, 그리고 (사건이 \(b’\)에서 일어난다고 가정했을 때) 다중도가 \(n\)일 확률이 곱해져있다. \(\sum^\infty_{n=1}P(n|b’)=1\) 그리고 정의상 \(\int^\infty_02\pi b’db’\rho(b’)=\sigma_\text{inel}\)이기 때문에, 식 (3)이 적절하게 정규화 돼(normalized) 있음을 확인할 수 있다. 다시말해 \(c(1)=1\)이다. 더 나아가, 중이온 충돌에서는 연속성 극한(continuity limit)을 사용해서 \(\sum^\infty_{n=N}\rightarrow\int^\infty_Ndn=\int^\infty_0dn\theta(n-N)\)과 같이 나타낼 수 있다.
\(P(n|b’)\)함수는 알려져 있지 않다. 하지만 입자 생성의 통계적인 특성과 여러가지 모델의 경험으로부터, 큰 \(n\)값에 대해 평균값 \(n(b’)\)주위에서 좁은 봉우리(peak)를 이룰것으로 기대된다. 따라서, 무한히 좁은 분포의 극한인, \(P(n|b’)=\delta[n-n(b’)]\)에서부터 시작해보도록 하자. 이 경우에는 다음과 같이 된다.
\[\begin{align}c(N)&=\int^\infty_0dn\theta(n-N)\int^\infty_0\frac{2\pi b’db’}{\sigma_\text{inel}}\rho(b’)\delta[n-n(b’)] \\ &=\int^\infty_0\frac{2\pi b’db’}{\sigma_\text{inel}}\rho(b’)\theta[n(b’)-N].\qquad\qquad(4)\end{align}\]
\(n(b’)\)이 \(b’\)에 대한 단조 감소 함수이기 때문에, \(n(b)=N\)의 해인 \(b(N)\)을 이용하여 \(\theta[n(b’)-N]=\theta[b(N)-b’]\)과 같이 나타낼 수 있다. 따라서,
\[\begin{align}c(N)&=\int^\infty_0\frac{2\pi b’db’}{\sigma_\text{inel}}\rho(b’)\theta[b(N)-b’] \\&=\int^{b(N)}_0\frac{2\pi b’db’}{\sigma_\text{inel}}\rho(b’)=\frac{\sigma_\text{inel}[b(N)]}{\sigma_\text{inel}}\qquad\qquad\text{(5)}\end{align}\]
이고, \(\sigma_\text{inel}[b(N)]\)은 \(0\leq b’\leq b(N)\)인 영역에서의 비탄성 충돌 단면적이다. 식 (5)는 식 (1)의 일반화된 공식이다. 참고자료 [11]의 Glauber 모형 내용에서 인용하였다. \(c\)와 \(b\)는 \(N\)에 의존하지만, 둘의 관계는 \(N\)에 직접적으로 의존하지 않는 것을 알 수 있다.
이제 분산 효과의 정량적인 분석으로 돌아오자. \(P(n|b’)\)을 다음과 같이 가정하자.
\[P(n|b’)=\frac{1}{\Delta n(b’)\sqrt{2\pi}}\exp\left(-\frac{[n-n(b’)]^2}{2\Delta n(b’)^2}\right).\qquad\text{(6)}\]
위 식은 \(\Delta n(b’)<n(b’)\)일 때의 좋은 근사가 된다. 그러면 \(c(N)\)은 다음과 같아진다.
\[c(N)=\int^\infty_0\frac{2\pi b’db’}{\sigma_\text{inel}}\rho(b’)\left\{\frac12\left[\mathrm{erf}\left(\frac{n(b’)-N}{\sqrt{2}\Delta n(b’)}\right)+1\right]\right\},\qquad\text{(7)}\].
작은 \(\Delta n(b’)\)에 대해, 중괄호 안에 있는 함수는 [washed out over the range \(\Delta n(b’)\)] \(\theta[n(b’)-N]\)과 같아진다. 따라서 다음과 같은 새로운 함수 \(d(x)\)를 도입한다.
\[d(x)=\frac12\left[\mathrm{erf}\left(\frac{x}{\sqrt{2}\Delta n}\right)+1\right]-\theta(x).\qquad\qquad\text{(8)}\]
\(d(x)\)를 임의의 함수 \(f(x)\)와 곱하여 적분 한 값을, 다음과 같이 \(\Delta n\)의 짝수 멱급수로 전개할 수 있다 (이것은 낮은 온도에서 Fermi-Dirac 분포의 Sommerfeld 전개와 [in spirit to] 비슷하다):
\[\int dx\,f(x)d(x)=-\sum_{j=1,3,5,\cdots}a_j(\Delta n)^{j+1}\left.\frac{d^jf(x)}{dx^j}\right|_{x=0},\qquad\text{(9)}\]
위 식에서 계수는 다음과 같다.
\[a_j=\frac1{j!}\int^\infty_{-\infty}dx\,x^jd(x)=\frac{2^{(j+3)/2}\Gamma\left(\dfrac j2+1\right)}{\sqrt{\pi}(j+1)!},\]
\[a_1=1,\quad a_3=\frac14,\quad a_5=\frac{1}{24},\quad a_7=\frac{1}{192},\quad\cdots\qquad\text{(10)}\]
식 (7)의 적분을 \(\int 2b’db’=\int dndb’^2/dn\)와 같이 바꾸고, 식 (9)의 전개를 이용하면 \(c(N)\)을 다음과 같이 적을 수 있다.
\[c(N)=\frac{\sigma_\text{inel}[b(N)]}{\sigma_\text{inel}}-[\Delta n(b(N))]^2\frac{d}{dn}\left.\left(\frac{\pi\rho[b(n)]}{\sigma_\text{inel}}\frac{db^2(n)}{dn}\right)\right|_{n=N}-\cdots.\qquad\text{(11)}\]
\(\rho(b(n))\simeq1\)인 안쪽 \(b\)에 대해서는 보정항이 \(d^2[b^2(n)]/dn^2\)에 비례한다. 아래에서 고려할 모형들에서는 이 양이 \(1/n^2\)에 비례하고, 그 결과 \(c(N)=\sigma_\text{inel}[b(N)]/\sigma_\text{inel}+O(\Delta n^2/n^2)])이 되며, 기하학적인 identification [식 (1) 또는 (5)] 가 좁은 분포에 대해 잘 맞음을 정량적으로 보여준다.
위 결과를 그려보고, 보정치의 더 상세한 수치 근사치를 얻기 위해, 우리는 두가지 모형을 생각할 것이다: wounded-mucleon 모형 [12] 에서 영감을 얻어낸 모델 하나와, 두 입자 충돌에 대한 Glauber 모형[13]의 광학적 한계가 그것이다. 반지름 \(r_0=(1.12A^{1/2}-0.86A^{-1/3})\text{ fm}\), \(A=197\), 그리고 너비 매개변수 \(a=0.54\text{ fm}\)을 가지고 Woods-Saxon로 기술되는 핵자 밀도 분포 \(\rho_A(r)\)를 가지고 금핵+금핵 반응을 볼 것이다. 핵-핵자 두께 함수는 \(T_a(s)=\int^\infty_{-\infty}dz\,\rho_A(\sqrt{s^2+z^2})\)로 주어지고, 상처입은 핵자들의 평균 수는
\[n(b)=2A\int^\infty_0s\,ds\int^{2\pi}_0d\varphi T_A(\sqrt{s^2+b^2+2sb\cos\varphi})\times\{1-[1-\sigma T_A(s)]^A\},\qquad\text{(12)}\]
로 주어진다. 참고자료 [14]를 따라서 핵자-핵자 비탄성 충돌 단면적은 \(\sigma=40\text{ mb}\)으로 할 것이다. 이 모형에서 얻어진 전체 핵-핵 충돌 단면적은 \(\sigma_\text{inel}=7.05\text{ b}\)이다. 주어진 \(b\)에서 생성된 상처입은 핵자들의 분산에 대한 표현은 매우 복잡하다. 다차원 적분을 계산하는 대신, 분명하게 보여주기 위해, \(\Delta n\sim n\)과 \(\Delta n\sim\sqrt{n}\)의 두 가지 경우에 대해 생각해 볼 것이다. 참고자료 [15]의 그림 1에 주어진 분포에 대한 표본 수치 결과로부터, (i) \(\Delta=n/10\) 또는 (ii) \(\Delta n=\sqrt{n}\)를 얻어낸다. 그림 1에서는, \(\rho(b’)=\theta(\sqrt{\sigma_\text{inel}/\pi}-b’)\)을 가지고 식 (7)과 (12)에 따라 \(c(N)\)을 (i)과 (ii)의 경우(각각 쇄선(dot-dashed line)과 점선)에 대해 계산한 결과를 보여준다. 이것들을, \(n(b)=N\)의 해로 정의되는 \(b(N)\)을 이용한 \(\pi b(N)^2/\sigma_\text{inel}\)(실선)와 함께 비교하고있다. 가장자리 충돌에 해당하는 매우 작은 \(N\,(N<2)\)의 매우 작은 영역과 \(b\)가 0주변에 해당하는 매우 큰 \(N\)의 영역을 제외하고는, 모든 선들이 선의 너비 안에 겹쳐있다. 큰 \(N\)에서의 차이는 \(b(N)\)을 만들 때 \(N=n(b=0)\approx377\)에서 0이 되도록 한 반면, \(c(N)\)을 상처입은 핵종의 최댓값이 \(N=2A\)이 될 때까지 0이 아닌 연속적인 값을 가지고 계산했기 때문에 발생한다. 이 효과는 그림 1의 (i)의 너비일 때에만 볼 수 있다.
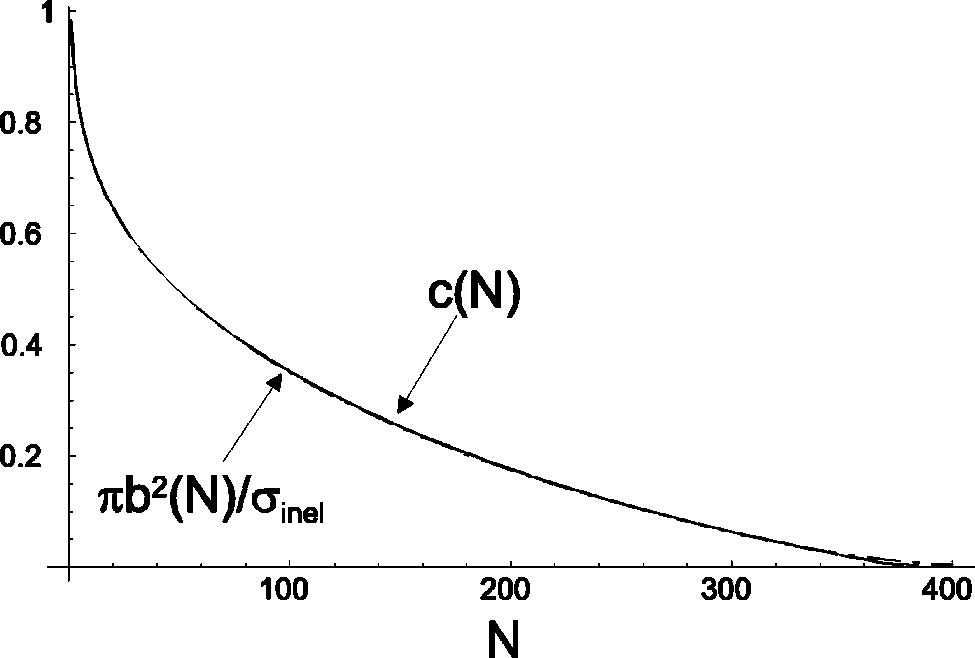
그림 2(a)의 결과처럼, 우리는 \(N\)의 의존성을 매개변수처럼 다뤄서 \(c[b(N)]\) vs. \(b(N)\)의 관계를 그릴 수 있다. 매우 가장자리 충돌(\(b>14\text{ fm}\))과 매우 중심 충돌(\(b<2\text{ fm}\))인 경우를 제외하고는, (i)와 (ii)의 선택에 대한 \(c(b)\)의 모형 선은 \(\pi b^2/\sigma_\text{inel}\)의 선과 또다시 겹친다. 이러한 모습은 그림 1의 모습을 직접적으로 반영한다. 중간정도의 \(b\)에서 식 (11)의 보정크기는 \(10^{-3}\)의 차수이다.
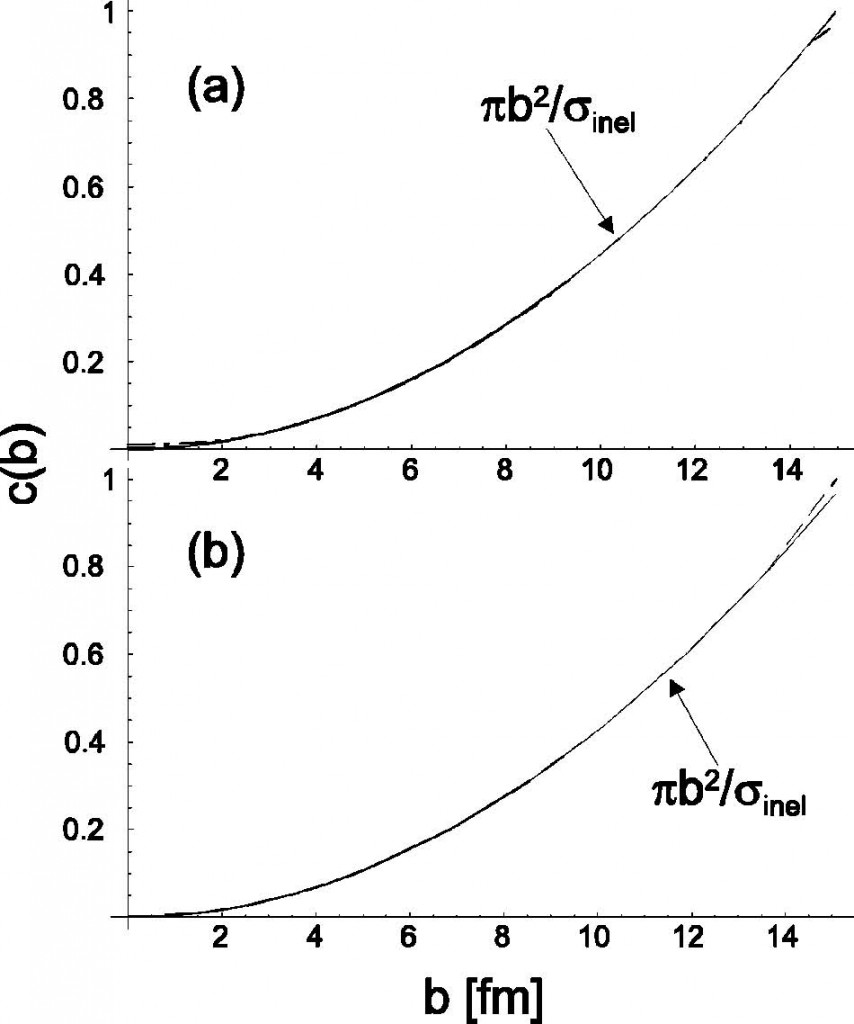
또 다른 실례로는 핵-핵 충돌의 Glauber 모형을 가지고 \(n=n_\text{coll}\)의 두 입자 충돌을 분석할 수 있다. 여기서는 간단한 표현식을 주는 모형의 광학적 제한을 사용한다. 이 모델에서
\[\begin{align}c(N)&=\sum^{A^2}_{n=N}\int^\infty_0\frac{2\pi b’ db’}{\sigma_\text{inel}}P_G(n,b’)\\&=\sum^{A^2}_{n=N}\int^\infty_0\frac{2\pi b’db’}{\sigma_\text{inel}}\left(\begin{matrix} A^2 \\ n \end{matrix}\right)[T(b’)\sigma]^n[1-T(b’)\sigma]^{A^2-n},\qquad\text{(13)}\end{align}\]
계속 번역 중
- PHOBOS Collaboration, B. B. Back et al., nucl-ex/0105011; Phys. Rev. Lett. 87, 102303 (2001).
- BRAHMS Collaboration, I. G. Bearden et al., Phys. Rev. Lett. 87, 112305 (2001); nucl-ex/0108016.
- J. Velkovska for the PHENIX Collaboration, nucl-ex/0105012; A. Bazilevsky for te PHENIX Collaboration, nucl-ex/0105017.
- J. W. Harris for the STAR Collaboration, in Ref. [5].
- Proceedings of Quark Matter 2001 conference, BNL, 2001 [Nucl. Phys. A (to be published)].
- STAR Collaboration, K. H. Ackermann et al., Phys. Rev. Lett. 86, 402 (2001).
- STAR Collaboration, C. Adler et al., nucl-ex/0107003.
- STAR Collaboration, C. Adler, Phys. Rev. Lett. 87, 082301 (2001).
- P. F. Kolb, U. Heinz, P. Huovinen, K. J. Eskola, and K. Tuominen, hep-ph/0103234.
- P. Huovinen, nucl-th/0108033.
- R. Vogt, Heavy Ion Phys. 9, 339 (1999).
- A. Białas, M. Błeszyński, and W. Czyż, Nucl. Phys. B111, 461 (1976).
- C.-Y. Wong, Introduction to High-Energy Heavy-Ion Collisions (World Scientific, Singapore, 1994).
- PHENIX Collaboration, K. Adcox et al., Phys. Rev. Lett. 86, 3500 (2001).
- A. Białas and B. Muryn, Acta Phys. Pol. B 18, 591 (1987).
독자들은, 비영리적인 개인으로써 자료를 보거나, 탐색하거나, 임시로 복사 할 목적으로만 사용할 수 있습니다. 이 자료는, 법에 규정되는 사항을 제외하고는 American Physical Society로부터의 서면 허가 없이 부분 혹은 전체를 재생산, 재배포, 전송, 수정, 전재, 수행, 전시, 출판 혹은 판매될 수 없습니다.
Translated with permission from Wojciech Broniowski and Wojciech Florkowski, Phys. Rev. C 65, 024905 (2002). Copyright 2012 by the American Physical Society.
Readers may view, browse, and/or download material for temporary copying purposes only, provided these uses are for noncommercial personal purposes. Except as provided by law, this material may not be further reproduced, distributed, transmitted, modified, adapted, performed, displayed, published, or sold in whole or part, without prior written permission from the American Physical Society.